Un árbol AVL (llamado así por las iniciales de sus inventores: Adelson-Velskii y Landis) es un árbol binario de búsqueda en el que para cada nodo, las alturas de sus subárboles izquierdo y derecho no difieren en más de 1.
No se trata de árboles perfectamente equilibrados, pero sí son lo suficientemente equilibrados como para que su comportamiento sea lo bastante bueno como para usarlos donde los ABB no garantizan tiempos de búsqueda óptimos.
El algoritmo para mantener un árbol AVL equilibrado se basa en reequilibrados locales, de modo que no es necesario explorar todo el árbol después de cada inserción o borrado.
Inserción
La inserción de un elemento en un árbol AVL es idéntica que en un árbol binario de búsqueda, la diferncia se encuentra en la comprobación que hay que realizar posteriormente en los árboles AVL.En un árbol AVL tras realizar la inserción hay que comprobar que se sigue manteniendo la condición de equilibrio, o lo que es lo mismo, que la altura del subárbol izquierdo y la del subárbol derecho difieran en una unidad o sean iguales. Si se produce un desequilibrio hay que re-equilibrar la estructura para que siga siendo un árbol AVL.
Vamos a ver los mecanismos de re-equilibrado de los árboles AVL:
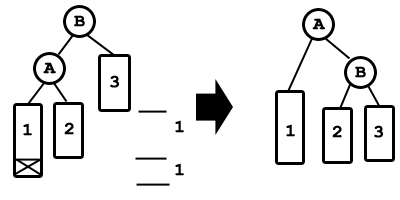
Rotación simple.
El nodo insertado es el marcado con una X. Esta inserción provoca un desequilibro en el nodo B, que se soluciona con esta rotación.
Borrar
El procedimiento de borrado es el mismo que en el caso de árboles binarios de búsqueda. La diferencia se encuentra en el proceso de reequilibrado posterior. Este proceso es idéntico al que se realiza en la inserción, la única diferencia es que en la inserción tras realizar una rotación el árbol ya estaba equilibrado, mientras que en el borrado puede ser necesario realizar mas de una rotación.Ejemplo:
Si eliminamos del siguiente árbol el nodo 3, el árbol se desequilibra en el nodo 2.
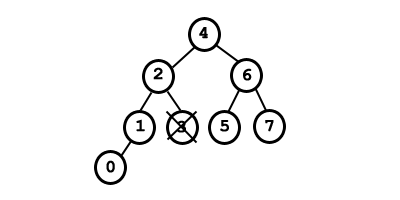
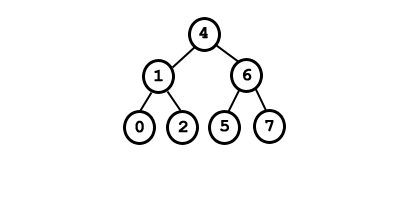
Después de eliminar el 3 el árbol resultante es:
VIDEO TUTORIAL DE ARBOLES AVL
No hay comentarios:
Publicar un comentario